Using custom states with BGLS

As mentioned in the Getting started guide, you can use BGLS with any representations of quantum states, so long as you specify how to apply_ops and compute_probability from these states. Here we show an example of this using a custom StateVector.

Setup

"""Setup."""
import itertools
from typing import Iterable, List

import numpy as np
import cirq

import bgls

Defining a custom state

First we create a custom quantum state type to use with BGLS, here a simple class for a state vector.

"""Define a custom quantum state representation to use with BGLS."""
class StateVector:
    """Representation of a state vector."""
    def __init__(self, num_qubits: int) -> None:
        """Initialize a StateVector.
        
        Args:
            num_qubits: Number of qubits in the state.
        """
        self.num_qubits = num_qubits
        self.vector = np.zeros(2**num_qubits, dtype=complex)
        self.vector[0] = 1. + 0.j
    
    def copy(self) -> "StateVector":
        """Returns a copy of the StateVector."""
        new_state = StateVector(self.num_qubits)
        new_state.vector = np.copy(self.vector)
        return new_state

Note: The copy method is required to use with BGLS.

For example, we can instantiate and use this class as follows.

state = StateVector(num_qubits=2)
state.vector

array([1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j])

Defining how to apply_ops

After defining a state, we need to be able to apply operations to it. Below we do this using matrix multiplication, first assuming matrices and vectors and then for Cirq operations acting on our StateVector above.

Note: The details of how to apply matrix gates aren’t the important takeaway here, but rather how to plug this into BGLS. So, this cell can be safely skimmed. When defining your own apply_op function, you’d write the equivalent of the following cell.

def apply_matrix_gate(gate: np.ndarray, target_bits: List[int], state: np.ndarray) -> None:
    """Applies a matrix gate to a state.
    
    Args:
        gate: The matrix of the gate to apply.
        target_bits: The (qu)bits the gate acts on.
        state: Wavefunction as a numpy array.
    """
    target_bits = target_bits[::-1]  # List of indices the gate is applied to.
    n = state.size  # For n qubits this is 2**n.

    # Flag whether we have worked on a given index already
    already_applied = np.zeros(n, dtype=int)
    for l in range(n):
        if already_applied[l]:
            continue
        subspace_indices = [l]
        for combo in powerset(target_bits):
            # E.g., [i0], [i1], [i0, i1], etc., one of these lists.
            if combo:  # Ignore the empty element.
                tempidx = l
                for bit in combo:
                    tempidx = flip_bit(tempidx, bit)
                subspace_indices.append(tempidx)

        apply_op_to_subspace(gate, state, np.asarray(subspace_indices))
        for idx in subspace_indices:
            already_applied[idx] = 1


# Helper functions for above.
def apply_op_to_subspace(gate: np.ndarray, state: np.ndarray, indices: np.ndarray) -> None:
    """Applies a matrix gate to a subspace.

    Args:
        gate: 2^q x 2^q numpy matrix, complex valued
        state: 2^n numpy array, complex valued
        indices: numpy array, integer valued, should be 2^q items in list
    """
    assert(indices.size == gate.shape[1])
    subspace = state[indices]
    output = gate.dot(subspace)
    state[indices] = output


def powerset(iterable: Iterable) -> itertools.chain:
    """Returns the powerset of an iterable."""
    s = list(iterable)
    return itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(len(s)+1))


def flip_bit(index: int, bit_to_flip: int) -> int:
    """Returns an integer equal to `index` but with the `i`th bit of index flipped,
    where `i` is `bit_to_flip`.

    Args:
        index: Integer to flip a bit of.
        bit_to_flip: Index of the bit in `index` to flip.
    """
    return index ^ (1 << bit_to_flip)

We can check that apply_matrix_gate works as intended for a simple Bell state preparation circuit.

apply_matrix_gate(cirq.unitary(cirq.H), target_bits=[0], state=state.vector)
print("StateVector after H:\t", state.vector)

apply_matrix_gate(cirq.unitary(cirq.CNOT), target_bits=[0, 1], state=state.vector)
print("StateVector after CNOT:\t", state.vector)

StateVector after H:	 [0.70710678+0.j 0.70710678+0.j 0.        +0.j 0.        +0.j]
StateVector after CNOT:	 [0.70710678+0.j 0.        +0.j 0.        +0.j 0.70710678+0.j]

Now we format this for BGLS as follows.

def apply_op(op: cirq.Operation, state: StateVector):
    """Applies the operation to the state, updating the state in place.
    
    Args:
        op: Operation to apply to the wavefunction.
        state: Wavefunction to apply the op to.
    """
    apply_matrix_gate(
        cirq.unitary(op.gate), 
        [q.x for q in sorted(op.qubits)], 
        state.vector
    )

Defining how to compute_probability

Last, we need to be able to compute the probability of any bitstring for the given state. We do this for the StateVector below by indexing.

def compute_probability(state: StateVector, bitstring: str):
    """Returns the probability of samplign the bitstring in the given state.
    
    Args:
        state: A 
        bitstring: 
    """
    return np.abs(state.vector[int(bitstring[::-1], 2)])**2

Using with BGLS

We can now use BGLS with our custom StateVector state, apply_op function, and compute_probability function.

"""Using the custom state with BGLS."""
# Example circuit to run.
a, b = cirq.LineQubit.range(2)
circuit = cirq.Circuit(
    cirq.H.on(a),
    cirq.CNOT.on(a, b),
    cirq.measure(a, b, key="z"),
)

# Create a BGLS simulator with the custom state.
sim = bgls.Simulator(
    initial_state=StateVector(num_qubits=2),
    apply_op=apply_op,
    compute_probability=compute_probability
)

# Run the circuit.
results = sim.run(circuit, repetitions=1000)
_ = cirq.plot_state_histogram(results)

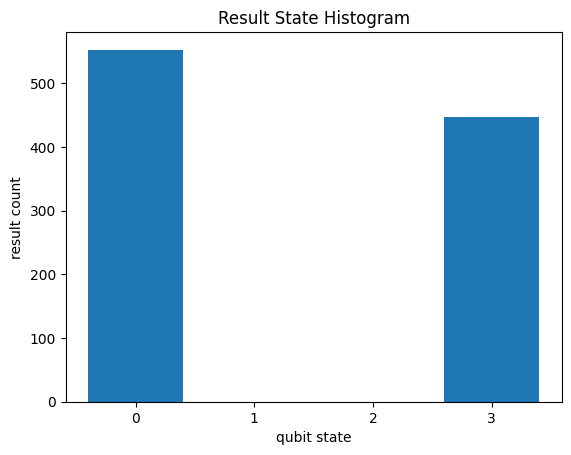
Note the returned results are formatted as usual for any Cirq circuit and the custom simulator supports all features supported by BGLS.