Features

BGLS supports several useful features when simulating circuits, described below.

"""Setup."""
import cirq

import bgls

Accessing final states

While measurement results (samples) are returned, final states are stored and can be accessed from bgls.Simulator.final_states as below.

a, b = cirq.LineQubit.range(2)

circuit = cirq.Circuit(
    cirq.H.on(a),
    cirq.CNOT.on(a, b),
    cirq.measure(a, b, key="z"),
)

sim = bgls.Simulator(
    initial_state=cirq.StateVectorSimulationState(
        qubits=(a, b), initial_state=0
    ),
    apply_op=cirq.protocols.act_on,
    compute_probability=bgls.born.compute_probability_state_vector,
)
results = sim.run(circuit, repetitions=10)
print("Results:", results)

final_state = sim.final_states[0]
print("Final state:", cirq.dirac_notation(final_state.target_tensor.flatten()))

Results: z=0000001111, 0000001111
Final state: 0.71|00⟩ + 0.71|11⟩

Note that here, although we sampled multiple times, there is only one final state.

len(sim.final_states)

1

This is because BGLS samples all bitstrings in parallel for unitary circuits. For circuits with non-unitary channels that are not terminal measurements (see below), the method of quantum trajectories is used and one bitstring is sampled per trajectory, leading to multiple final states.

Final state history can be reset as follows.

sim.clear_final_states()
sim.final_states

[]

Simulating noisy circuits

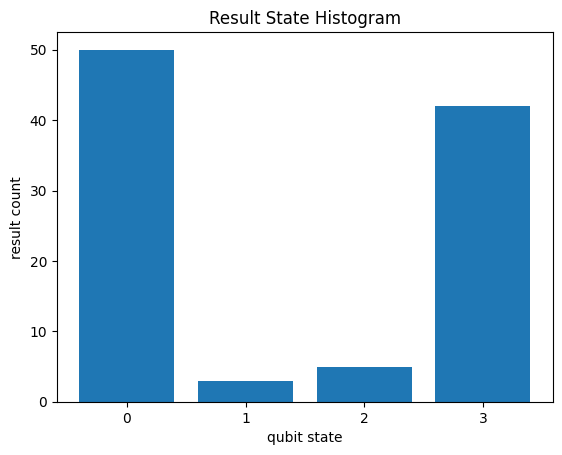
If your apply_op function can apply channels, you can use BGLS to simulate noisy circuits through quantum trajectores. An example using cirq.protocols.act_on, which can apply channels, is shown below.

a, b = cirq.LineQubit.range(2)

circuit = cirq.Circuit(cirq.H.on(a), cirq.CNOT.on(a, b))
noisy = circuit.with_noise(cirq.depolarize(0.05))

sim = bgls.Simulator(
    initial_state=cirq.StateVectorSimulationState(
        qubits=(a, b), initial_state=0
    ),
    apply_op=cirq.protocols.act_on,
    compute_probability=bgls.born.compute_probability_state_vector,
)

results = sim.run(noisy + cirq.measure(a, b), repetitions=100)
cirq.plot_state_histogram(results);

How to modify apply_op to support channels

You can modify your apply_op function to support channels as follows. The simplest case is when the probability of a Kraus operator does not depend on the state. In this case, you can use the cirq.mixture protocol to obtain (probability, kraus_operator) pairs as in the example below.

channel = cirq.DepolarizingChannel(p=0.01)

cirq.mixture(channel)

((0.99,
  array([[1., 0.],
         [0., 1.]])),
 (0.0033333333333333335,
  array([[0.+0.j, 1.+0.j],
         [1.+0.j, 0.+0.j]])),
 (0.0033333333333333335,
  array([[0.+0.j, 0.-1.j],
         [0.+1.j, 0.+0.j]])),
 (0.0033333333333333335,
  array([[ 1.+0.j,  0.+0.j],
         [ 0.+0.j, -1.+0.j]])))

Now, you just need to select a Kraus operator according to the probability distribution and then apply it to the state.

If the channel does not support the cirq.mixture protocol (i.e., if the probability of applying a Kraus operator depends on the state \(|\psi\rangle\)), you can still use this method by first using cirq.kraus to obtain the Kraus operators \(K_i\) of the channel, then computing the probability of applying each channel via \(p_i = \langle \psi | K_i^\dagger K_i |\psi\rangle\).

Note: For noiseless simulation, BGLS updates all bitstrings in parallel via one evolution of the state. This isn’t possible in quantum trajectories because many different states are generated, so you should expect noisy simulation to be slower.

Simulating circuits with intermediate measurements

In the same manner described above, BGLS can simulate circuits with intermediate measurements if apply_op supports channels.

a, b = cirq.LineQubit.range(2)

circuit = cirq.Circuit(
    cirq.H.on(a),
    cirq.measure(a),  # <-- Intermediate measurement.
    cirq.CNOT.on(a, b),
    cirq.measure(a, b),
)

sim.clear_final_states()
results = sim.run(circuit, repetitions=10)
cirq.plot_state_histogram(results);

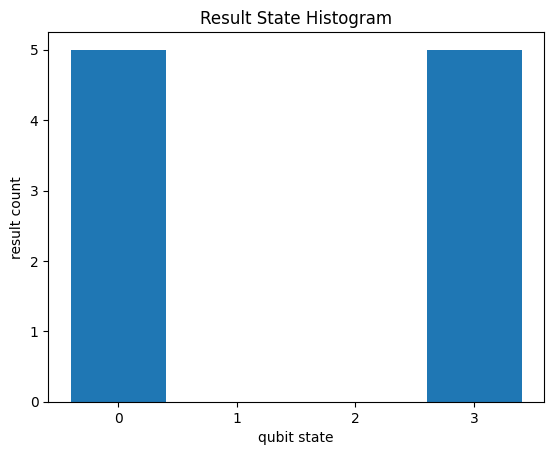
Here the final states are \(|00\rangle\) or \(|11\rangle\) with equal probability.

for final_state in sim.final_states:
    print(f"Final state:", cirq.dirac_notation(final_state.target_tensor.flatten()))

Final state: |00⟩
Final state: |00⟩
Final state: |00⟩
Final state: |00⟩
Final state: |11⟩
Final state: |11⟩
Final state: |11⟩
Final state: |11⟩
Final state: |00⟩
Final state: |11⟩

Can I use BGLS with Qiskit / Pennylane / etc.?

The only accepted circuit type for BGLS is cirq.Circuit, but you can convert most popular circuit types to and from Cirq. For example, if you have a Qiskit circuit specified by the following Qasm string:

qasm = """
OPENQASM 2.0;
include "qelib1.inc";

qreg q[2];

h q[0];
cx q[0],q[1];"""

You can convert this to a Cirq circuit as follows.

from cirq.contrib.qasm_import import circuit_from_qasm

circuit_from_qasm(qasm)

q_0: ───H───@───
            │
q_1: ───────X───

This circuit can now be used with BGLS.