Using BGLS with MPS to solve QAOA problems

For large sparse graphs, we expect matrix product states to be particularly efficient being that their runtime scales primarily in the (sparse) degree of connectedness. Here we will use such states with our bgls sampler to solve the MaxCut problem for random graphs.

import time

import numpy as np
import matplotlib.pyplot as plt

import sympy

import networkx as nx

import cirq
import cirq.contrib.quimb as ccq
import cirq.contrib.quimb.mps_simulator
from cirq.contrib.svg import SVGCircuit

import quimb.tensor as qtn

import bgls

Here we define a function to compute bitstring amplitudes for a matrix product state. (Note, this is the same as found in mps_simulation)

def cirq_mps_bitstring_probability(
        mps: cirq.contrib.quimb.MPSState, bitstring: str
) -> float:
    """
    Returns the probability of measuring the `bitstring` (|z⟩) in the
    'cirq.contrib.quimb.MPSState' mps.
    Args:
        mps: Matrix Product State as a 'cirq.contrib.quimb.MPSState'.
        bitstring: Bitstring |z⟩ as a binary string.
    """
    M_subset = []
    for i, Ai in enumerate(mps.M):
        qubit_index = mps.i_str(i)
        # selecting the component with matching bitstring:
        A_subset = Ai.isel({qubit_index: int(bitstring[i])})
        M_subset.append(A_subset)

    tensor_network = qtn.TensorNetwork(M_subset)
    bitstring_amplitude = tensor_network.contract(inplace=False)
    return np.power(np.abs(bitstring_amplitude), 2)

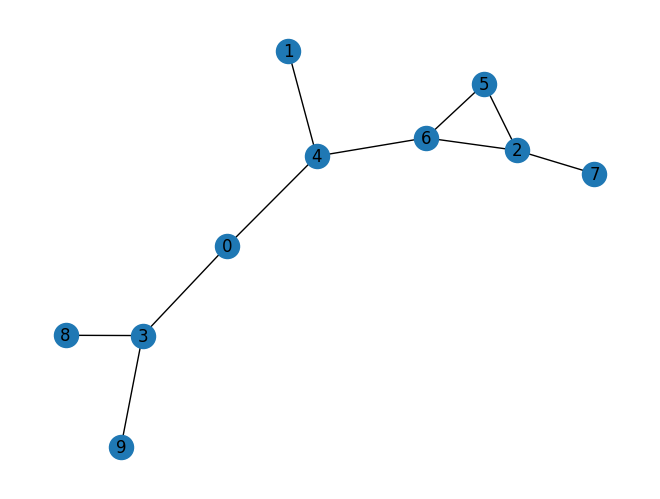
We first create a random graph with n nodes and connectivity p

n = 10
p = 0.3
rand_graph = nx.erdos_renyi_graph(n, p, seed=2)
nx.draw(rand_graph, with_labels=True)

We then implement the cost hamiltonian translated to qubits \(H_c = \frac{1}{2}\sum(1-Z_iZ_j)\), parametrized as \(U_c=e^{i\gamma H_c}\), as well as the mixing hamiltonian \(H_m = \sum X_i\), parametrized as \(U_m=e^{i\beta H_m}\).

def config_energy(assignments, graph):
    energy = 0.
    for (i, j) in graph.edges:
        energy += 1 - (assignments[i] * assignments[j])
    energy /= 2
    return energy


def obj_func(result, graph):
    # return the average energy for a results repetitions
    def config_energy(assignments):
        energy = 0.
        for (i, j) in graph.edges:
            energy += 1 - (assignments[i] * assignments[j])
        energy /= 2
        return energy

    assignments = 2 * result.measurements.get("z") - 1  # convert to +- 1
    return np.average(
        [config_energy(assignment) for assignment in assignments])


def Uc(graph, gamma):
    for (i, j) in graph.edges:
        yield cirq.ZZ.on(cirq.LineQubit(i), cirq.LineQubit(j)) ** gamma


def Um(graph, beta):
    for i in graph.nodes:
        yield cirq.X.on(cirq.LineQubit(i)) ** beta


def construct_circuit(graph, p_range, gammas, betas):
    circuit = cirq.Circuit()
    for i in graph.nodes:
        circuit.append(cirq.H.on(cirq.LineQubit(i)))
    for p in range(p_range):
        circuit.append(Uc(graph, gammas[p]))
        circuit.append(Um(graph, betas[p]))
    circuit.append(
        cirq.measure(cirq.LineQubit.range(len(graph.nodes)), key='z'))
    return circuit

g1 = sympy.Symbol("g1")
b1 = sympy.Symbol("b1")

maxcut_circuit = construct_circuit(rand_graph, 1, [g1], [b1])
SVGCircuit(maxcut_circuit)

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

findfont: Font family 'Arial' not found.

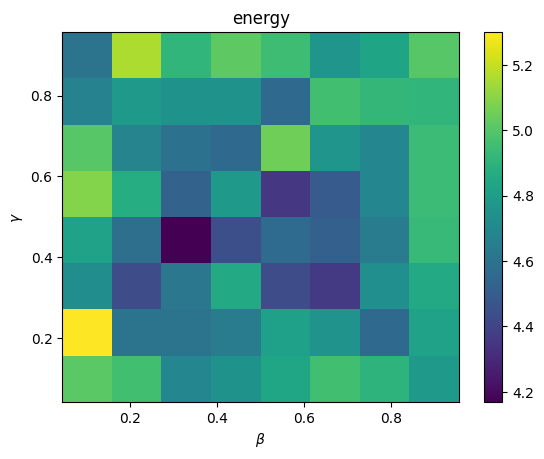
We find the optimal values of gamma and beta by sweeping across parameter combinations. Sampling repeatedly from the resultant circuits, and computing the final average energy for each, we pick the combination minimizing the energy. We can make use of symbols to call cirq’s run_sweep across a range of settings.

ngammas = 8
nbetas = 8
param_sweep = (cirq.Linspace(key='g1', start=0.1, stop=0.9,
                             length=ngammas) * cirq.Linspace(key='b1',
                                                             start=0.1,
                                                             stop=0.9,
                                                             length=nbetas))


class LowChi(cirq.contrib.quimb.MPSOptions):
    max_bond = 3


bgls_mps_sampler = bgls.Simulator(
    cirq.contrib.quimb.MPSState(
        qubits=maxcut_circuit.all_qubits(), initial_state=0,
        prng=np.random.RandomState(), simulation_options=LowChi()
    ),
    cirq.act_on,
    cirq_mps_bitstring_probability,
    seed=1
)

results = bgls_mps_sampler.run_sweep(maxcut_circuit, params=param_sweep,
                                     repetitions=100)

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[7], line 1
----> 1 results = bgls_mps_sampler.run_sweep(maxcut_circuit, params=param_sweep,
      2                                      repetitions=100)

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/cirq/sim/simulator.py:72, in SimulatesSamples.run_sweep(self, program, params, repetitions)
     69 def run_sweep(
     70     self, program: 'cirq.AbstractCircuit', params: 'cirq.Sweepable', repetitions: int = 1
     71 ) -> Sequence['cirq.Result']:
---> 72     return list(self.run_sweep_iter(program, params, repetitions))

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/cirq/sim/simulator.py:103, in SimulatesSamples.run_sweep_iter(self, program, params, repetitions)
    101         records[protocols.measurement_key_name(op)] = np.empty([0, 1, 1])
    102 else:
--> 103     records = self._run(
    104         circuit=program, param_resolver=param_resolver, repetitions=repetitions
    105     )
    106 yield study.ResultDict(params=param_resolver, records=records)

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/bgls/simulator.py:125, in Simulator._run(self, circuit, param_resolver, repetitions)
    122 param_resolver = param_resolver or cirq.ParamResolver()
    123 resolved_circuit = cirq.resolve_parameters(circuit, param_resolver)
--> 125 return self._sample(resolved_circuit, repetitions)

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/bgls/simulator.py:148, in Simulator._sample(self, circuit, repetitions)
    143 keys_to_bitstrings_list = []
    145 if not needs_trajectories(circuit):
    146     # Sample all bitstrings in one pass through the circuit.
    147     keys_to_bitstrings_list = (
--> 148         self._sample_from_one_wavefunction_evolution(
    149             circuit, repetitions
    150         )
    151     )
    152 else:
    153     # Sample one bitstring per trajectory.
    154     for _ in range(repetitions):

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/bgls/simulator.py:219, in Simulator._sample_from_one_wavefunction_evolution(self, circuit, repetitions)
    215 self._apply_op(op, state)
    217 # Skip updating bitstrings for diagonal gates since they do not change
    218 # the probability distribution.
--> 219 if all(cirq.is_diagonal(kraus) for kraus in cirq.kraus(op)):
    220     continue
    222 # Memoize self._compute_probability.

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/cirq/protocols/kraus_protocol.py:154, in kraus(val, default)
    151     return tuple(np.sqrt(p) * u for p, u in mixture_result)
    153 unitary_getter = getattr(val, '_unitary_', None)
--> 154 unitary_result = NotImplemented if unitary_getter is None else unitary_getter()
    155 if unitary_result is not NotImplemented and unitary_result is not None:
    156     return (unitary_result,)

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/cirq/ops/gate_operation.py:195, in GateOperation._unitary_(self)
    193 getter = getattr(self.gate, '_unitary_', None)
    194 if getter is not None:
--> 195     return getter()
    196 return NotImplemented

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/cirq/ops/eigen_gate.py:342, in EigenGate._unitary_(self)
    340     return NotImplemented
    341 e = cast(float, self._exponent)
--> 342 return np.sum(
    343     [
    344         component * 1j ** (2 * e * (half_turns + self._global_shift))
    345         for half_turns, component in self._eigen_components()
    346     ],
    347     axis=0,
    348 )

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/numpy/core/fromnumeric.py:2313, in sum(a, axis, dtype, out, keepdims, initial, where)
   2310         return out
   2311     return res
-> 2313 return _wrapreduction(a, np.add, 'sum', axis, dtype, out, keepdims=keepdims,
   2314                       initial=initial, where=where)

File /opt/hostedtoolcache/Python/3.11.5/x64/lib/python3.11/site-packages/numpy/core/fromnumeric.py:88, in _wrapreduction(obj, ufunc, method, axis, dtype, out, **kwargs)
     85         else:
     86             return reduction(axis=axis, out=out, **passkwargs)
---> 88 return ufunc.reduce(obj, axis, dtype, out, **passkwargs)

KeyboardInterrupt: 

We then find the combo with minimum energy by searching over all pairs

energies = np.zeros(shape=(ngammas, nbetas))
max_energy = None
max_params = None
for i, result in enumerate(results):
    energy = obj_func(result, rand_graph)
    energies[int(i / ngammas), i % nbetas] = energy
    if max_energy == None or energy > max_energy:
        max_energy = energy
        max_params = result.params

plt.pcolormesh(np.linspace(0.1, 0.9, ngammas), np.linspace(0.1, 0.9, nbetas),
               energies, shading="nearest")
plt.colorbar()
plt.xlabel(r"$\beta$")
plt.ylabel(r"$\gamma$");
plt.title("energy")

Text(0.5, 1.0, 'energy')

print("max energy: ", max_energy)
print("at params: ", max_params)

max energy:  5.3
at params:  cirq.ParamResolver({'g1': 0.2142857142857143, 'b1': 0.1})

Finally we fix the maximized parameters, repeatedly sample at this configuration, and then take as our graph solution the measurement with maximal energy.

result_at_max = bgls_mps_sampler.run_sweep(maxcut_circuit, params=max_params,
                                           repetitions=1000)

best_energies = np.zeros(shape=(ngammas, nbetas))
max_best_energy = None
best_assignment = None
for i, result in enumerate(result_at_max):
    for assignment in 2 * result.measurements.get("z") - 1:
        energy = config_energy(assignment, rand_graph)
        best_energies[int(i / ngammas), i % nbetas] = energy
        if max_best_energy == None or energy > max_best_energy:
            max_best_energy = energy
            best_assignment = assignment

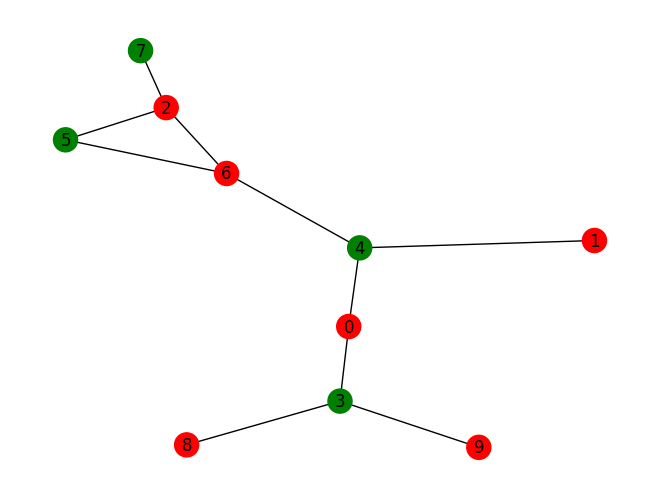
print("max best energy i.e. number of slices: ", max_best_energy)
print("with system configuration: ", best_assignment)

max best energy i.e. number of slices:  9.0
with system configuration:  [-1. -1.  1.  1.  1. -1. -1. -1. -1. -1.]

nodesa = [0, 1, 2, 6, 8, 9]
nodesb = [3, 4, 5, 7]
subset_color = ["red", "green"]

g = nx.Graph()
for n in rand_graph.nodes():
    if n in nodesa:
        g.add_node(node_for_adding=n, attr={'l': 0})
    else:
        g.add_node(node_for_adding=n, attr={'l': 1})
for a, b in rand_graph.edges:
    g.add_edge(a, b)

colors = [subset_color[data['attr']['l']] for v, data in g.nodes(data=True)]

nx.draw(g, node_color=colors, with_labels=True)